An Introduction to Investment Theory
© William N. GoetzmannYALE School of Management
Chapter I: Capital Markets and Investment Performance
Overview
Suppose you find a great investment opportunity, but you lack the cash to take advantage of it. This is the classic problem of financing. The short answer is that you borrow -- either privately from a bank, or publicly by issuing securities. Securities are nothing more than promises of future payment. They are initially issued through financial intermediaries such as investment banks, which underwrite the offering and work to sell the securities to the public. Once they are sold, securities can often be re-sold. There is a secondary market for many corporate securities. If they meet certain regulatory requirements, they may be traded through brokers on the stock exchanges, such as the NYSE, the AMEX and NASDAQ, or on options exchanges and bond trading desks.
Securities come in a bewildering variety of forms - there are more types of securities than there are breeds of cats and dogs, for instance. They range from relatively straightforward to incredibly complex. A straight bond promises to repay a loan over a fixed amount of interest over time and the principal at maturity. A share of stock, on the other hand, represents a fraction of ownership in a corporation, and a claim to future dividends. Today, much of the innovation in finance is in the development of sophisticated securities: structured notes, reverse floaters, IO's and PO's -- these are today's specialized breeds. Sources of information about securities are numerous on the world-wide web. For a start, begin with the Ohio State Financial Data Finder. All securities, from the simplest to the most complex, share some basic similarities that allow us to evaluate their usefulness from the investor's perspective. All of them are economic claims against future benefits. No one borrows money that they intend to repay immediately; the dimension of time is always present in financial instruments. Thus, a bond represents claims to a future stream of pre-specified coupon payments, while a stock represents claims to uncertain future dividends and division of the corporate assets. In addition, all financial securities can be characterized by two important features: risk and return. These two key measures will be the focus of this second module.
I. Finance from the Investor's Perspective
Most financial decisions you have addressed up to this point in the term have been from the perspective of the firm. Should the company undertake the construction of a new processing plant? Is it more profitable to replace an old boiler now, or wait? In this module, we will examine financial decisions from the perspective of the purchaser of corporate securities: shareholders and bondholders who are free to buy or sell financial assets. Investors, whether they are individuals or institutions such as pension funds, mutual funds, or college endowments, hold portfolios, that is, they hold a collection of different securities. Much of the innovation in investment research over the past 40 years has been the development of a theory of portfolio management, and this module is principally an introduction to these new methods. It will answer the basic question, What rate of return will investors demand to hold a risky security in their portfolio? To answer this question, we first must consider what investors want, how we define return, and what we mean by risk.
II. Why Investors Invest
What motivates a person or an organization to buy securities, rather than spending their money immediately? The most common answer is savings -- the desire to pass money from the present into the future. People and organizations anticipate future cash needs, and expect that their earnings in the future will not meet those needs. Another motivation is the desire to increase wealth, i.e. make money grow. Sometimes, the desire to become wealthy in the future can make you willing to take big risks. The purchase of a lottery ticket, for instance only increases the probability of becoming very wealthy, but sometimes a small chance at a big payoff, even if it costs a dollar or two, is better than none at all. There are other motives for investment, of course. Charity, for instance. You may be willing to invest to make something happen that might not, otherwise -- you could invest to build a museum, to finance low-income housing, or to re-claim urban neighborhoods. The dividends from these kinds of investments may not be economic, and thus they are difficult to compare and evaluate. For most investors, charitable goals aside, the key measure of benefit derived from a security is the rate of return.
III. Definition of Rates of Return
The investor return is a measure of the growth in wealth resulting from that investment. This growth measure is expressed in percentage terms to make it comparable across large and small investors. We often express the percent return over a specific time interval, say, one year. For instance, the purchase of a share of stock at time t, represented as Pt will yield P t+1 in one year's time, assuming no dividends are paid. This return is calculated as: R t = [ P t+1 - Pt]/ Pt. Notice that this is algebraically the same as: Rt= [P t+1/ Pt]-1. When dividends are paid, we adjust the calculation to include the intermediate dividend payment: Rt=[ P t+1 - Pt+Dt]/ Pt. While this takes care of all the explicit payments, there are other benefits that may derive from holding a stock, including the right to vote on corporate governance, tax treatment, rights offerings, and many other things. These are typically reflected in the price fluctuation of the shares.
IV. Arithmetic vs. Geometric Rates of Return
There are two commonly quoted measures of average return: the geometric and the arithmetic mean. These rarely agree with each other. Consider a
two period example: P0 = $100,
R1 = -50% and R2 = +100%. In this case, the
arithmetic average is calculated as (100-50)/2 = 25%, while the geometric
average is calculated as: [(1+R1)(1+R2)]1/2-1=0%. Well, did you make money over the two periods, or not? No, you didn't, so the geometric average is closer to investment experience. On the other hand, suppose R1 and R2 were statistically representative of future returns. Then next year, you have a 50% shot at getting $200 or a 50% shot at $50. Your expected one year return is (1/2)[(200/100)-1] + (1/2)[(50/100)-1] = 25%. Since most investors have a multiple year horizon, the geometric return is useful for evaluating how much their investment will grow over the long-term. However, in many statistical models, the arithmetic rate of return is employed. For mathematical tractability, we assume a single period investor horizon.
V. Capital Market History
The 1980's was one of the greatest decades for stock investors in the history of the U.S. capital markets.

(Courtesy Ibbotson Associates)
The 1930's was one of the worst decades for U.S. stock investors.

(Courtesy Ibbotson Associates)
U.S. Capital Markets over the Long Term: 1926 - 1995
Over the past 68 years, A stock investment in the S&P increased from $1 to $800

(Courtesy Ibbotson Associates)
VI. Risk Premium
Notice in the preceding figure that a dollar invested in stock grew to $889 over the period, while a dollar invested in corporate bonds grew to $40. Why the big difference? This return differential is commonly attributed to a difference in the risk associated with stocks as opposed to bonds. Notice that the stock line is "shakier" than the bond line. Wealth invested in stocks since 1926 was more volatile than wealth invested in bonds. Despite the higher return, the risks were higher as well. An investor typically cares about the riskiness of an investment. If, for instance, you are saving for a home purchase sometime in the next year, then you really care whether your $100,000 nest egg has a significant probability of dropping to $50,000 in twelve months. As a matter of fact, you might be willing to trade a lower rate of investment return for "insurance" that your principal will be secure. This is called risk-aversion -- and all things being equal, most investors prefer less risk to more.
| Investment | geom. mean | arith.mean | std | high ret. | low ret. |
| S&P total return | 10.30 | 12.45 | 22.28 | 42.56 | -29.73 |
| U.S. Small Stock TR | 12.28 | 17.28 | 35.94 | 73.46 | -36.74 |
| U.S. LT Govt TR | 4.91 | 5.21 | 8.00 | 15.23 | -8.41 |
| U.S. LT Corp. TR | 5.49 | 5.73 | 7.16 | 13.76 | -8.90 |
| U.S. 30 day T-Bills | 3.70 | 3.70 | .96 | 1.35 | -0.06 |
The difference between the S&P total return and the U.S. 30 day T-Bill return is called the equity premium. It is the amount of return that investors demand for holding a risky security such as stocks, as opposed to a riskless security, such as T-Bills. The annual equity premium is about 9% arithmetic, and 6% geometric, over the 1926 - 1995 period.
VII. Standard Deviation as a Measure of Risk
Stock returns may be riskier or more volatile, but this concept is a difficult one to express simply. To do so, we borrow a concept from statistics, called standard deviation. standard deviation is a summary measure about the average spread of observations. It is the square root of the variance, which is calculated as:
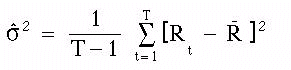
The standard deviation of one-year S&P 500 returns is about 22.28%. If S&P returns are normally distributed, this means that about 2/3 of the time we should observe an annual return within the range (12.45-22.28)= -9.93 and (12.45+22.28)= 34.73. A histogram of S&P 500 annual returns shows that returns are approximately normally distributed, or are they? A normal distribution should allow returns lower than -100%. Stocks do not. In fact, the log of the variable being normally distributed is a better approximation. However, there is evidence to suggest that even this is not quite right. The tails of stock returns are a bit "fatter" than should be observed if returns were log-normally distributed. This lends some support to the hypothesis advanced by Benoit Mandelbrot that stock returns follow a "stable" distribution, with undefined variance. Have a look at the S&P 500 histogram yourself:

How well does standard deviation capture the notion of investor risk? It equally weights high returns with low returns. It heavily weights extreme observations. It is not concerned with the shape of the distribution. All of these are valid criticisms. However the benefits to using standard deviation are large. It is a single measure, allowing us to quantify asset returns by risk. As we will see in the next chapter, it also provides the basis for investor decisions about portfolio choice.
See if you can:
- find historical return information on Microsoft, Inc.
- find historical return information on the Fidelity Magellan Fund
- identify the top five investment banks in the U.S.
- find which company on the S&P 500 had the largest capital appreciation return last year
- find the current yields on U.S. treasury bonds
If you accept the challenge, email me with your list of http sites!
Next Chapter| |Will's Home Page| MPPM 540 Main Menu| Table of Contents|Mail Will|
 © William N. Goetzmann
© William N. Goetzmann
YALE School of Management